Atomic Spectroscopy Lock
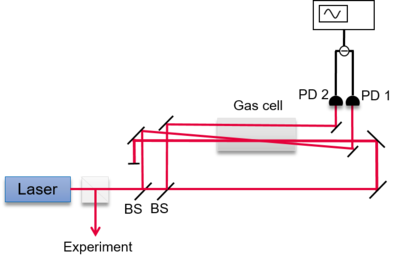
A straightforward optical setup for realizing a spectroscopy lock was already discussed in the application note “Frequency References”. However, to get rid of the Doppler broadening, a different setup is needed and sketched in Figure 7. A beam derived from the laser to be stabilized is split into two parts using a beam splitter (BS). Most of the light is transmitted and is called the pump beam. Only a small fraction (typically around 10%) of the light is reflected and is called probe beam. The beams are guided such that probe and pump beam are In some realizations a telescope is used to widen the pump beam such that the probe beam has large overlap with the pump beam inside the gas cell.counter-propagating. Behind the gas cell the intensity of the probe beam is recorded with a photo diode (PD). If the pump beam is blocked and the laser frequency is scanned, i.e. changed over time, then the Doppler broadened peak shown in Figure 8 (a) is recorded. If the pump beam is on, however, narrow peaks on top of the Doppler broadened profile occur, shown in Figure 8 (b), which correspond to the Hyperfine levels of the atoms. This is because, as mentioned above, the velocity of the atoms is governed by probability and therefore a fraction of the atoms happen to have almost zero velocity. Therefore, if the laser hits the resonance of a Hyperfine level the strong pump beam saturates the atomic gas, i.e. the atoms are not able to absorb further photons. Therefore the probe beam will be transmitted. If the laser frequency is off-resonant, e.g. detuned to a lower frequency, only atoms will be excited which counter-propagate the laser light with a velocity matching the Doppler shift. As probe and pump beam counter-propagate, both lasers excite atoms which move in opposite directions. Therefore, the group of atoms that is excited by the probe beam is not the same group of atoms that is in resonance with the pump beam. Consequently, the transmission of the probe beam is unchanged by the presence of the pump beam if the laser frequency is not on resonance with the unshifted atomic transition.
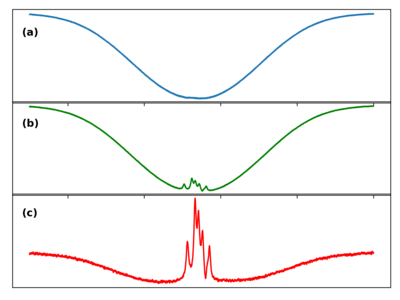
The Doppler broadened transmission of a second probe beam which is sent through the gas cell without overlapping the pump beam can be used as a reference. Subtracting this reference from the actual signal yields the signal shown in Figure 8 (c).
TOPTICA Solution
TOPTICA´s CoSy includes a complete optical setup for Doppler-free saturation spectroscopy together with a controller which performs the subtraction of the reference signal from the spectroscopy signal. The laser light is simply fed to the CoSy via a fibre, so no alignment is necessary. The subtracted signal is available at one of the output ports of the controller.
TOPTICA Solution
Both options of generating the error signal from the spectroscopy signal are supported by TOPTICA´s DLC pro Lock, which is a software option of TOPTICA´s laser controller DLC pro and will be further discussed in the application note "PID Feedback Controllers”. It offers the possibility to choose between side-of-fringe and top-of-fringe locking. In the case of side-of-fringe locking it internally performs the subtraction of an adjustable constant value. In the case of top-of-fringe locking it performs the modulation of the laser current. Alternatively, it provides a signal which can be used to generate the phase or frequency modulation using e.g. an electro-optic modulator (EOM). Beyond that, it also performs the demodulation of the spectroscopy signal to yield the error signal shown in Figure 6. Together with the CoSy, the DLC pro Lock integrated in the DLC pro offers one of the most convenient ways of error signal generation. This combination is all you need to stabilize the frequency of TOPTICA´s diode lasers. The clear and simple setup needed for realizing an atomic spectroscopy lock is sketched in Figure 10.
Considering one hyperfine peak of this spectroscopy signal, an error signal can be generated following one of the methods described in the sections “a) Side-of-fringe locking” and “b) FM spectroscopy and top-of-fringe locking”. In both options the error signal indicates how much the laser frequency deviates from a set point. Therefore we refer to locks which are based on these error signals as frequency locks.


