Phase and Frequency of Laser Light
Laser light can be described by its space and time-dependent electric field E(x,t). For the purpose of discussing phase and frequency locking of lasers, the spatial dependence is not of relevance and will be neglected. Therefore, a perfect monochromatic light field can be written as
\(E(t)=\frac{1}{2}A\cdot\exp{\left(-2\pi i\bar{\nu}t\right)} + c.c.\)
where A is the amplitude and \(\bar{\nu}\) the frequency of the light field. The abbreviation “c.c.” stands for the complex conjugate of the preceding expression. In fact, various noise sources lead to fluctuations of the laser frequency \(\nu(t)=\bar{\nu}+\tilde{\nu}(t) \) and of the amplitude A(t), where ν is the light field´s mean frequency and \(\tilde{\nu}(t)\) represents time-dependent fluctuations, such that
\(E(t)=\frac{1}{2}A(t)\cdot\exp{\left(-i\left(2\pi\bar{\nu}t+\tilde{\varphi}(t)\right)\right)}+c.c.\)
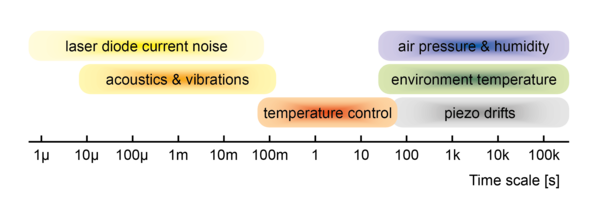
where the quantity \(\tilde{\varphi}(t)=2\pi\int_0^t{\tilde{\nu}(t)du}\) describes phase fluctuations. In this application note only frequency fluctuations \(\tilde{\nu}(t)\) are considered while the amplitude At is assumed to be constant. Figure 2 shows several causes for frequency fluctuations and the corresponding time scales on which they occur.
A signal which is typically considered to visualize a laser´s frequency stability is the laser spectrum \(\mathcal{L}(f)\). It is the absolute square of the Fourier transform of the time-dependent electric field. The full width at half maximum (FWHM) of the spectral feature is referred to as laser linewidth and is often quoted as a measure for a laser´s frequency stability. The exact value of the linewidth not only depends on the laser itself but also on the corresponding measurement time. If the electric field is only recorded over several microseconds, considering Figure 2, it is clear that fluctuations like air pressure changes which occur on a time scale of several seconds do not contribute to the single-shot linewidth but rather manifest themselves as a drift or jitter of the central frequency of subsequent measurements. Typical causes for frequency drifts and jitter are changes of the environment, e.g. air pressure, humidity and temperature and changes related to the laser system like piezo drifts and imperfections of the temperature control.
Strictly speaking, the laser linewidth does not contain all information about the noise properties of a laser. A more detailed picture is offered by the power spectral density (PSD) of the phase or frequency noise, which are the absolute square of the Fourier transforms of \(\tilde{\varphi}(t)\) and \(\tilde{\nu}(t)\) respectively.